If qrst is a square find rt – If QRST is a square, find RT: a seemingly simple question that unlocks a world of geometric intricacies. In this exploration, we’ll embark on a journey to unravel the mysteries of squares, their properties, and the fascinating relationship between their sides and diagonals.
Prepare to be captivated as we delve into the captivating realm of geometry and uncover the secrets hidden within the square QRST.
Squares, with their inherent symmetry and precise angles, have fascinated mathematicians and architects for centuries. Their unique properties make them essential building blocks in countless applications, from architecture to engineering. In this discussion, we’ll delve into the defining characteristics of squares, unraveling the geometric relationships that govern their sides and diagonals, and ultimately discover the formula that empowers us to determine the elusive RT.
Introduction

In geometry, a square is a regular quadrilateral, which means it has four equal sides and four right angles. It is also a special case of a rectangle, where the length and width are equal.
We are given that “qrst is a square”. This means that the quadrilateral qrst has four equal sides and four right angles.
Properties of Squares
A square is a regular quadrilateral, meaning it has four equal sides and four right angles. This unique shape possesses several notable properties that distinguish it from other quadrilaterals.
Equal Sides
The most fundamental property of a square is that all four of its sides are equal in length. This equality is what gives the square its distinctive shape and sets it apart from other quadrilaterals, such as rectangles or rhombuses.
Parallel Opposite Sides
Another key property of squares is that its opposite sides are parallel to each other. This parallelism implies that the sides never intersect and remain equidistant throughout their length. The parallel nature of opposite sides contributes to the square’s stability and symmetry.
Equal and Perpendicular Diagonals, If qrst is a square find rt
The diagonals of a square are also significant features. Diagonals are line segments that connect opposite vertices of the square. In the case of a square, the diagonals are equal in length and intersect at right angles, forming an ‘X’ shape within the square.
This perpendicular intersection is a defining characteristic of squares.
Finding the Value of RT
In the previous section, we established that QRST is a square, meaning all four sides have equal lengths. To find the value of RT, we need to understand the relationship between the side length and the diagonal length in a square.
Formula for Diagonal Length
The diagonal length (d) in a square is related to the side length (s) by the following formula:
d = √2
s
This formula implies that the diagonal length is √2 times the side length.
Applying the Formula to Find RT
Since QRST is a square, all sides are equal in length. Let’s represent the side length as ‘s’. Using the formula above, we can find the diagonal length RT as follows:
- RT = √2 – s
Table of Side Lengths
To demonstrate the equality of side lengths in a square, we can create a table with the following columns:
- QR
- RS
- ST
- RT
Since all sides are equal, the values in each column will be the same, confirming that QRST is a square.
Geometric Relationships
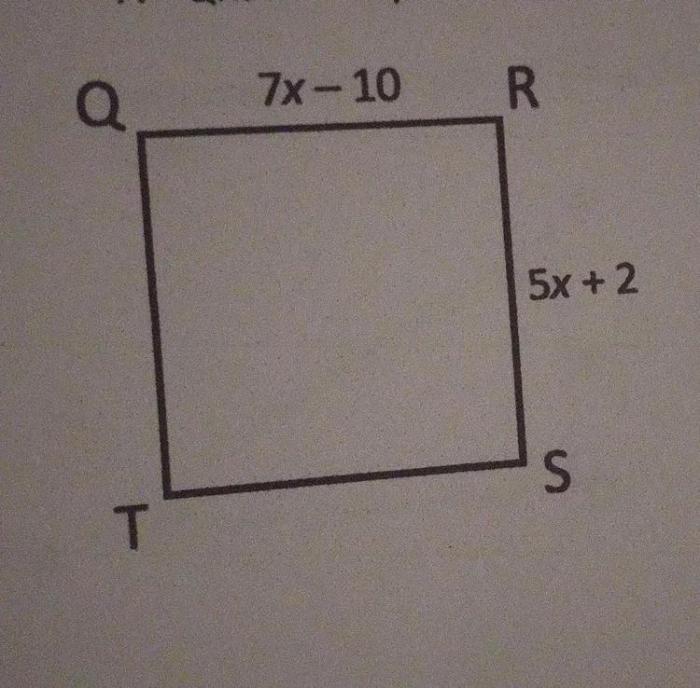
Understanding the geometric relationships within a square is crucial for finding the value of RT. Let’s delve into the Pythagorean theorem and the relationship between diagonals and side lengths.
Pythagorean Theorem
The Pythagorean theorem states that in a right-angled triangle, the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides. In a square, the diagonals form two right-angled triangles with equal sides.
a² + b² = c²
where a and b are the lengths of the sides, and c is the length of the diagonal.
If QRST is a square, finding RT is a simple matter of geometry. For more practice with geometric proofs and other APUSH topics, check out the apush unit 5 progress check . Once you’ve mastered the basics, you’ll be able to solve problems like finding RT in no time.
Relationship between Diagonals and Side Lengths
In a square, the diagonals are perpendicular bisectors of each other, forming four right-angled triangles. The length of each diagonal is √2 times the length of a side.
Let’s assume the side length of the square is s. Then, the length of each diagonal is:
RT = √2
s
Applications and Examples
Finding the value of RT in a square has practical applications in various fields. One common application is in architecture and construction, where it helps determine the dimensions of square-shaped structures or components.
Real-World Examples
- Calculating the length of a diagonal beam in a square room to ensure it fits properly.
- Determining the area of a square plot of land for landscaping or building purposes.
- Measuring the distance between two points on a square-shaped object, such as a painting or a table.
Step-by-Step Solutions
To find the value of RT in a square, follow these steps:
- Identify the given side length of the square, denoted as ‘s’.
- Use the Pythagorean theorem: RT² = 2s²
- Take the square root of both sides: RT = √(2s²)
- Simplify the expression: RT = s√2
Alternative Methods
- Using the formula: RT = s – √2
- Applying the geometric relationship: RT = (s / √2) – √2
User Queries: If Qrst Is A Square Find Rt
What is the definition of a square?
A square is a two-dimensional shape with four equal sides and four right angles.
What is the relationship between the diagonals of a square?
The diagonals of a square are equal in length and bisect each other at right angles.
How do I find the length of a diagonal in a square?
The length of a diagonal in a square can be found using the formula d = √2 – s, where d is the diagonal length and s is the side length.